Visualizing Tumor Response using Waterfall Charts with R

Author

Sophia Z. Shalhout, David M. Miller

Published

May 9, 2020

Abstract

Visualizing Tumor Response using Waterfall Charts with R

Key points

This monograph provides a reference resource for creating waterfall plots in R which may be useful in depicting the tumor response to treatment of each patient for example, enrolled in an oncology clinical trial.
- We provide an overview of how to create waterfall plots which may be useful for publications, and presentations using R.
- We outline the steps to presenting the patients nonrandomly, but in descending order, on the plot from the worst response to the best response for appropriately visualizing the waterfall plot.
- In oncology, a waterfall plot will present the response of each subject with the x- axis set at baseline measurements, and vertical bars added per subject either above or below the horizontal axis representing increase in tumor burden or decrease in tumor burdern respectively.
Skill Level: Intermediate
- Assumption made by this post is that readers have some familiarity with basic R.

Let’s load the packages we will use.

library(tidyverse)
library(dplyr)
library(knitr)

Merkel Cell Carcinoma- Example Oncology Clinical Trial Data Set

Let’s first create an “example” data set for demonstrative purposes for subjects with locally advanced or distantly metastatic Merkel Cell Carcinoma (MCC) enrolled on a clinical trial that aims to test the effects of treatment A on tumor response at two different doses.

# We will first create a data set that specifies patients with locally advanced/unresectable MCC and metastatic disease.

# Waterfall plots are displayed in descending order from the worst tumor response from baseline value on the left to the best value on the right side of the plot
## Therefore, we will create data for 55 subjects and order them in decreasing order since a positive value here represents increase in tumor size from baseline and a negative value represents a decrease in size.

# We will randomly assign the two doses, 80 mg or 150 mg, to the 56 subjects
Merkel <- data.frame(
  id=c(1:56), 
  type = sample((rep(c("laMCC", "metMCC"), times =28))), 
  response = c(30, sort(runif(n=53,min=-10,max=19), decreasing=TRUE),-25,-31), 
  dose= sample(rep(c(80, 150), 28)))

# Let's assign Best Overall Response (BOR)
Merkel$BOR= (c("PD", rep(c("SD"), times =54),"PR"))

Let’s view the data set

kable((Merkel))

id	type	response	dose	BOR
1	laMCC	30.0000000	150	PD
2	laMCC	18.7563667	150	SD
3	metMCC	18.2765383	80	SD
4	laMCC	17.6844494	150	SD
5	laMCC	17.0075271	150	SD
6	metMCC	16.7150357	80	SD
7	laMCC	16.2368676	150	SD
8	laMCC	14.7904273	80	SD
9	metMCC	14.3057887	150	SD
10	metMCC	14.1024327	80	SD
11	laMCC	14.0896363	150	SD
12	laMCC	13.7805769	80	SD
13	metMCC	13.0401910	150	SD
14	laMCC	13.0091003	80	SD
15	metMCC	12.7355414	150	SD
16	laMCC	12.5705367	80	SD
17	laMCC	11.4021159	150	SD
18	metMCC	11.1845503	80	SD
19	laMCC	9.7695614	150	SD
20	metMCC	9.4971918	80	SD
21	metMCC	9.4470578	80	SD
22	metMCC	8.9701755	80	SD
23	metMCC	8.8002298	150	SD
24	laMCC	8.6923195	80	SD
25	laMCC	8.2005430	150	SD
26	laMCC	7.9385936	80	SD
27	metMCC	7.0426535	150	SD
28	laMCC	6.7676051	80	SD
29	laMCC	6.5310004	150	SD
30	metMCC	6.3448264	150	SD
31	laMCC	5.5842064	80	SD
32	metMCC	5.5300945	80	SD
33	laMCC	5.4826064	80	SD
34	laMCC	5.3608580	80	SD
35	metMCC	4.9056868	80	SD
36	metMCC	4.2141766	80	SD
37	metMCC	2.8333400	150	SD
38	laMCC	2.6977406	150	SD
39	metMCC	0.7587159	80	SD
40	metMCC	0.4850728	150	SD
41	laMCC	0.3984248	80	SD
42	laMCC	0.2778293	80	SD
43	metMCC	-0.5827850	150	SD
44	laMCC	-0.6818098	150	SD
45	metMCC	-0.9533467	150	SD
46	laMCC	-1.3104243	150	SD
47	metMCC	-3.8226207	150	SD
48	laMCC	-4.1856408	80	SD
49	metMCC	-6.4087922	150	SD
50	metMCC	-7.0850612	150	SD
51	metMCC	-8.4744712	150	SD
52	metMCC	-9.0152615	80	SD
53	metMCC	-9.1460582	80	SD
54	laMCC	-9.7198343	150	SD
55	laMCC	-25.0000000	80	SD
56	metMCC	-31.0000000	80	PR

Let’s create the waterfall plot.

MCC<- barplot(Merkel$response, 
              col="blue", 
              border="blue", 
              space=0.5, ylim=c(-50,50), 
              main = "Waterfall plot for Target Lesion Tumor Size", 
              ylab="Change from baseline (%)",
              cex.axis=1.5, cex.lab=1.5)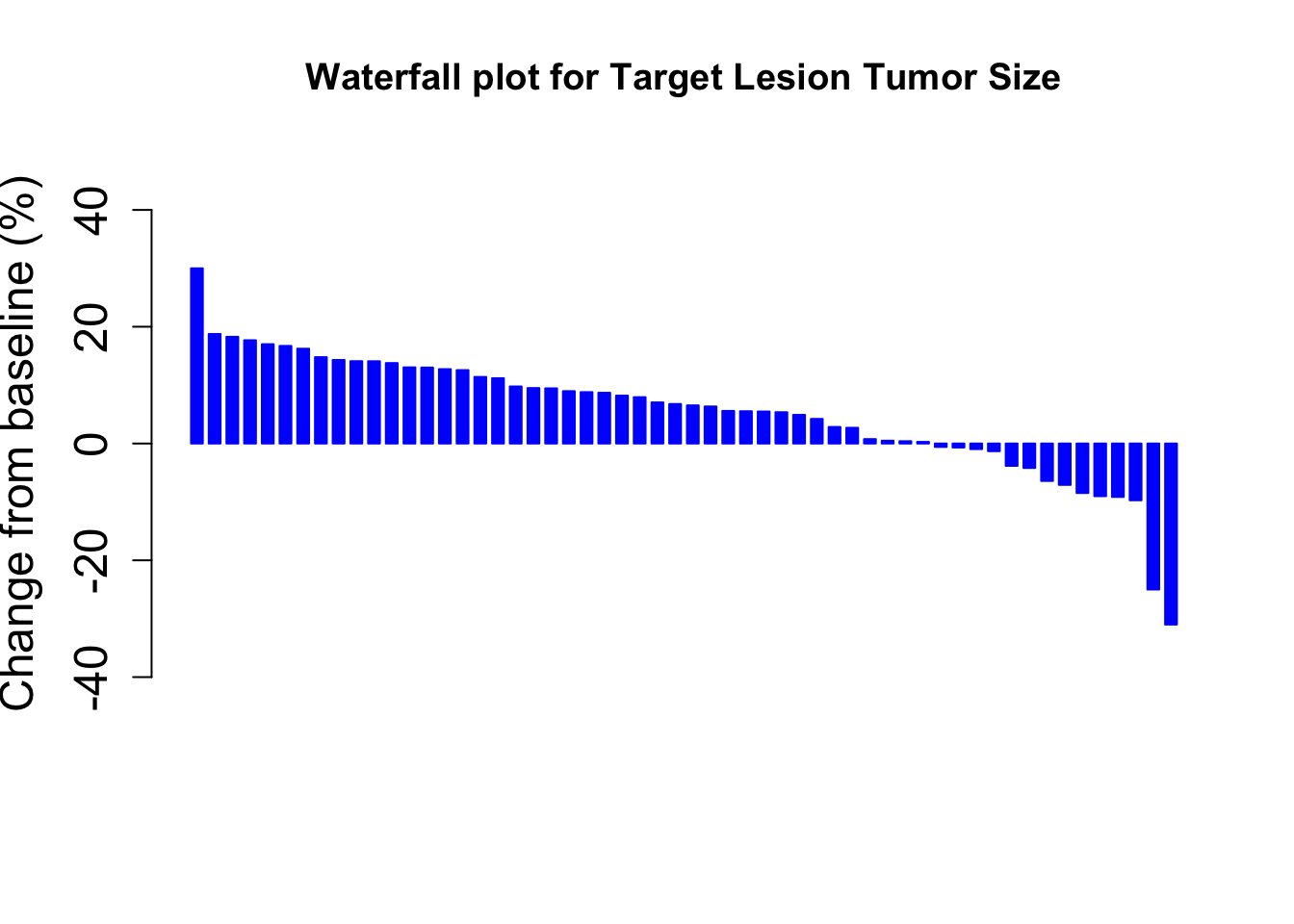

We can now add color by Dose and a legend

col <- ifelse(Merkel$dose == 80, 
              "steelblue", # if dose = 80 mg, then the color will be steel blue
              "cadetblue") # if dose != 80 mg (i.e. 150 mg here), then the color will be cadet blue

MCC<- barplot(Merkel$response, 
              col=col, 
              border=col, 
              space=0.5, 
              ylim=c(-50,50),
              main = "Waterfall plot for Target Lesion Tumor Size", 
              ylab="Change from baseline (%)",
              cex.axis=1.5, 
              legend.text= c( "80mg", "150mg"),
              args.legend=list(title="Treatment Dose", fill=c("steelblue", "cadetblue"), border=NA, cex=0.9))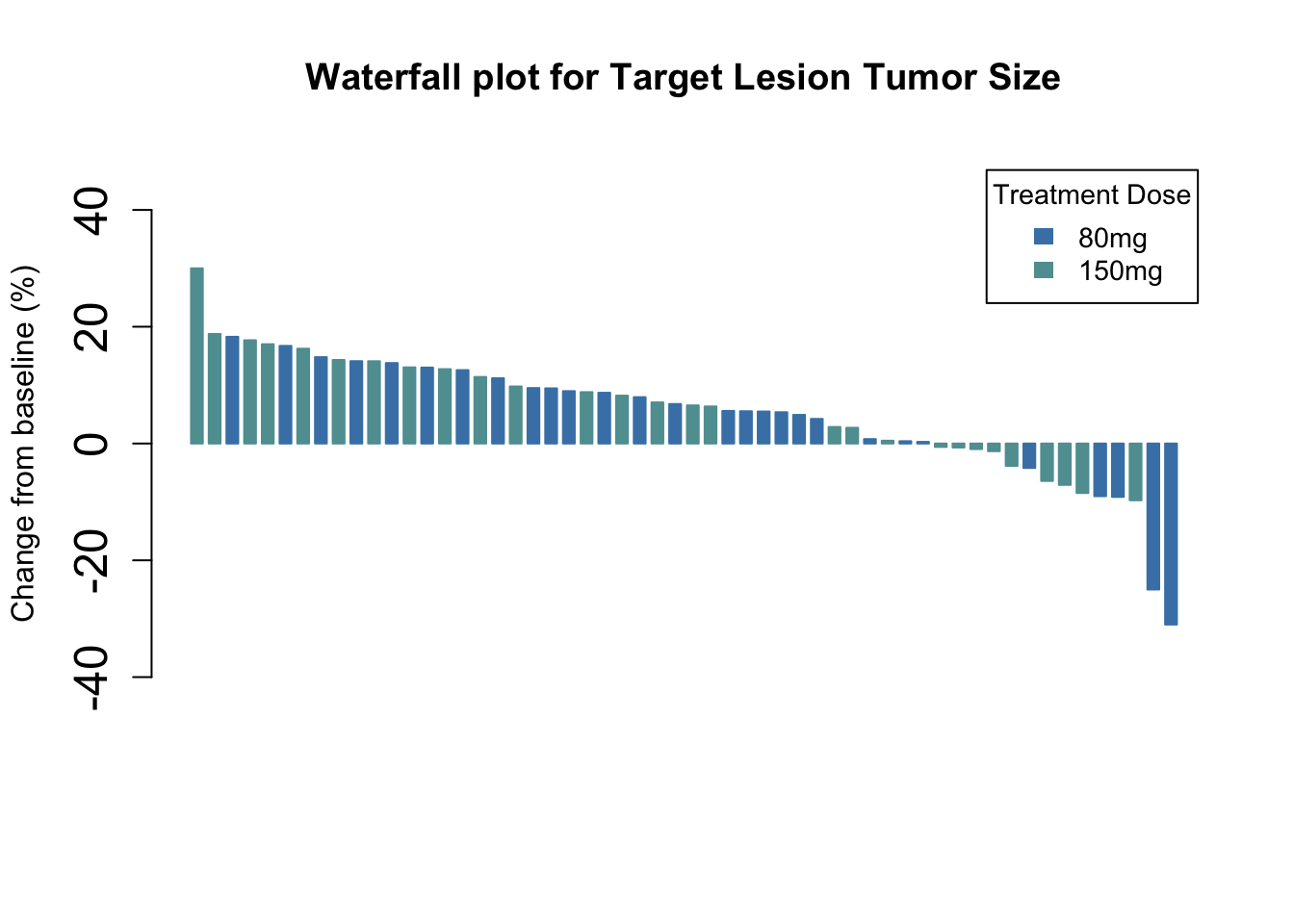

Or by disease type…

col <- ifelse(Merkel$type == "laMCC", 
              "#BC5A42", # if type of disease = locally MCC, then the color will be #BC5A42 (deep red)
              "#009296") # if type of disease != locaally MCC (i.e. mMCC), then the color will be ##009296 (greenish-blue)

MCC<- barplot(Merkel$response, 
              col=col, 
              border=col, 
              space=0.5, 
              ylim=c(-50,50),
              main = "Waterfall plot for Target Lesion Tumor Size", 
              ylab="Change from baseline (%)",
              cex.axis=1.5, 
              legend.text= c( "locally advanced MCC", "Metastatic MCC"),
              args.legend=list(title="Disease", fill=c("#BC5A42", "#009296"), border=NA, cex=0.9))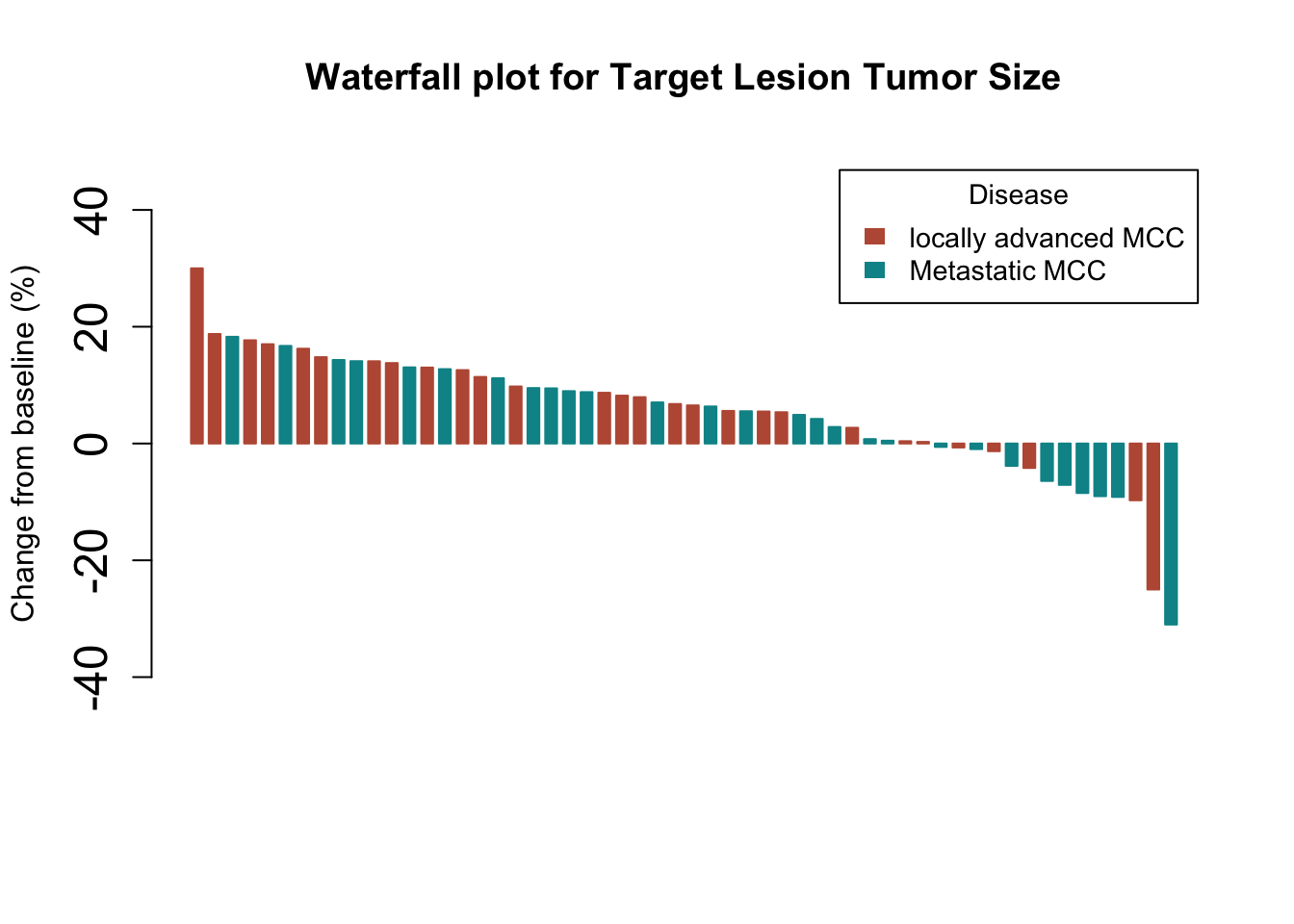

Or by Best overall response and provide a legend

col <- ifelse(Merkel$BOR == "CR", 
              "green", # if a subject had a CR the bar will be green, if they did not have a CR....
              ifelse(Merkel$BOR == "PR", 
                     "steelblue", # then, if a subject had a PR the bar will be steel blue, if they did not have a PR or CR....
                     ifelse(Merkel$BOR == "PD", 
                            "red", # then, if a subject had a PD the bar will be red, otherwise if they did not have a PR or CR or PD.... 
                            ifelse(Merkel$BOR == "SD", 
                                   "cadetblue", # then they must have ahd a SD, so the bar will be cadetblue, otherwise....
                                   "") # the color will be blank (which is not really an option, b/c they must have either a CR, PR, PD or SD)
                            )))

              
MCC<- barplot(Merkel$response, 
              col=col, 
              border=col, 
              space=0.5, 
              ylim=c(-50,50),
              main = "Waterfall plot for Target Lesion Tumor Size", ylab="Change from baseline (%)",
              cex.axis=1.5, 
              legend.text= c( "CR: Complete Response", "PR: Partial Response", "SD: Stable Disease", "PD: Progressive Disease"),
              args.legend=list(title="Best Overall Response", fill=c("green","steelblue",  "cadetblue", "red"), border=NA, cex=0.9))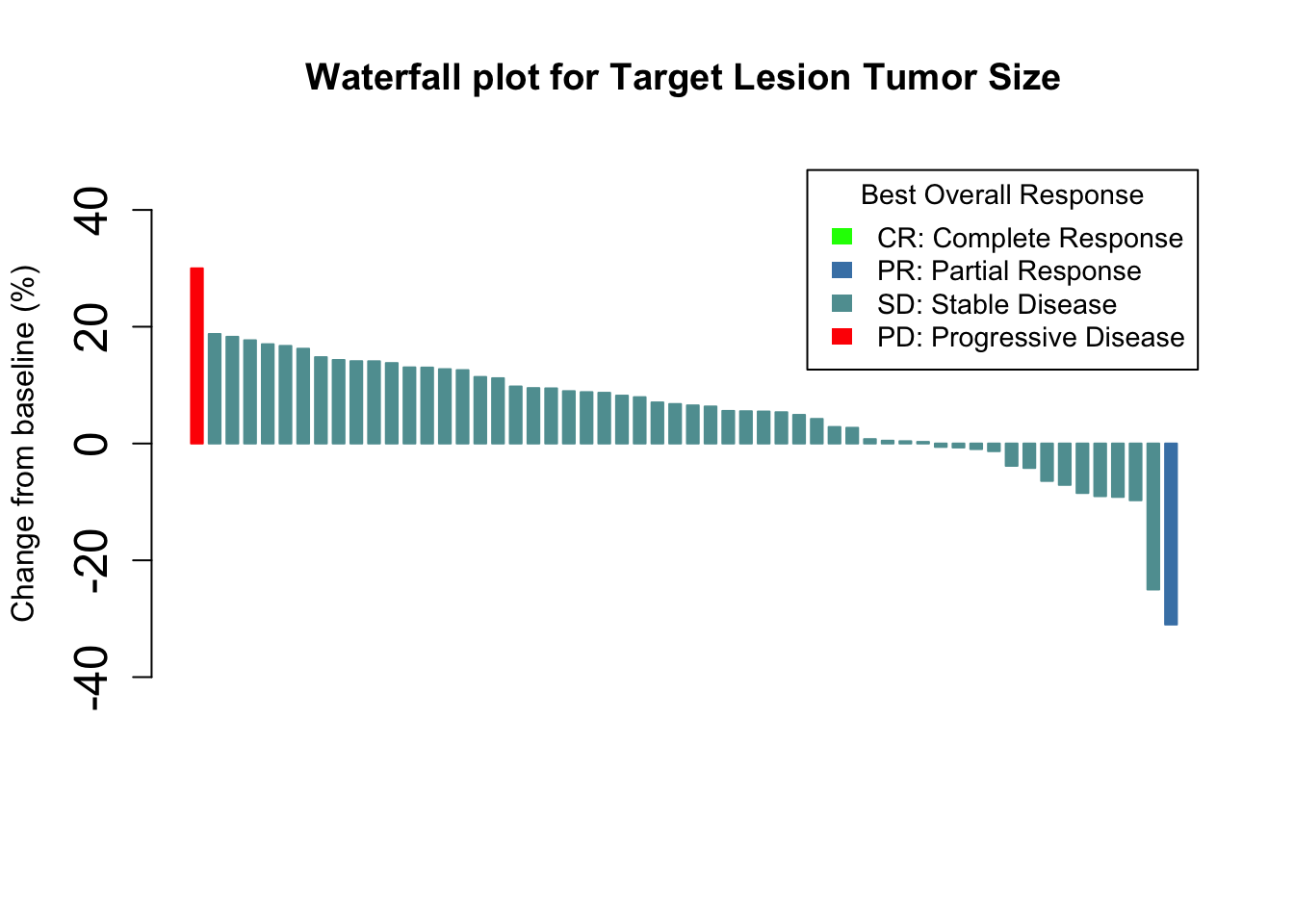

Let’s add horizontal lines at 20% and -30%

The majority of clinical trials use the Response Evaluation Criteria in Solid Tumors (RECIST) to assess tumor responses to a therapeutic intervention
Per RECIST, tumor responses are adjudicated based on the following observations:
- Complete Response (CR) Disappearance of all target lesions (sum of all taget lesions = 0)
  - Of note, any pathological lymph nodes (whether target or non-target) must have a reduction in size to < 10 mm
- Partial Response (PR) >= 30% decrease (vs baseline) of sum of all target lesions dimension
- Progressive Disease (PD) new lesions or >= 20% increase (vs smallest sum of target lesions or nadir)
- Stable Disease (SD) when sum of all target lesions does not qualify for CR/PR/PD
Thus, it is often useful to have lines to denote “Progressive Disease” and “Partial Response” on waterfall plots
- Those bars between the PD and PR lines denote “Stable Disease”

col <- ifelse(Merkel$BOR == "CR", 
              "green",
              ifelse(Merkel$BOR == "PR", 
                     "steelblue",
                     ifelse(Merkel$BOR == "PD", 
                            "red", 
                            ifelse(Merkel$BOR == "SD", 
                                   "cadetblue", ""))))

MCC<- barplot(Merkel$response, 
              col=col, 
              border=col, 
              space=0.5, 
              ylim=c(-50,50),
              main = "Waterfall plot for Target Lesion Tumor Size",
              ylab="Change from baseline (%)",
              cex.axis=1.5, 
              legend.text= c( "CR: Complete Response", "PR: Partial Response", "SD: Stable Disease", "PD: Progressive Disease"),
              args.legend=list(title="Best Overall Response", fill=c("green","steelblue",  "cadetblue", "red"), border=NA, cex=1.0))

# Use the abline() function
## The abline() function is a simple way to add lines in R
### It takes the arguments: abline(a=NULL, b=NULL, h=NULL, v=NULL, ...)
#### a, b : single values denoting the intercept and the slope of the line
#### h : the y-value(s) for horizontal line(s)
#### v : the x-value(s) for vertical line(s)

abline(h=20, col = "black", lwd=0.5) # The "PD" line
abline(h=-30, col = "black", lwd=0.5) # This "PR" line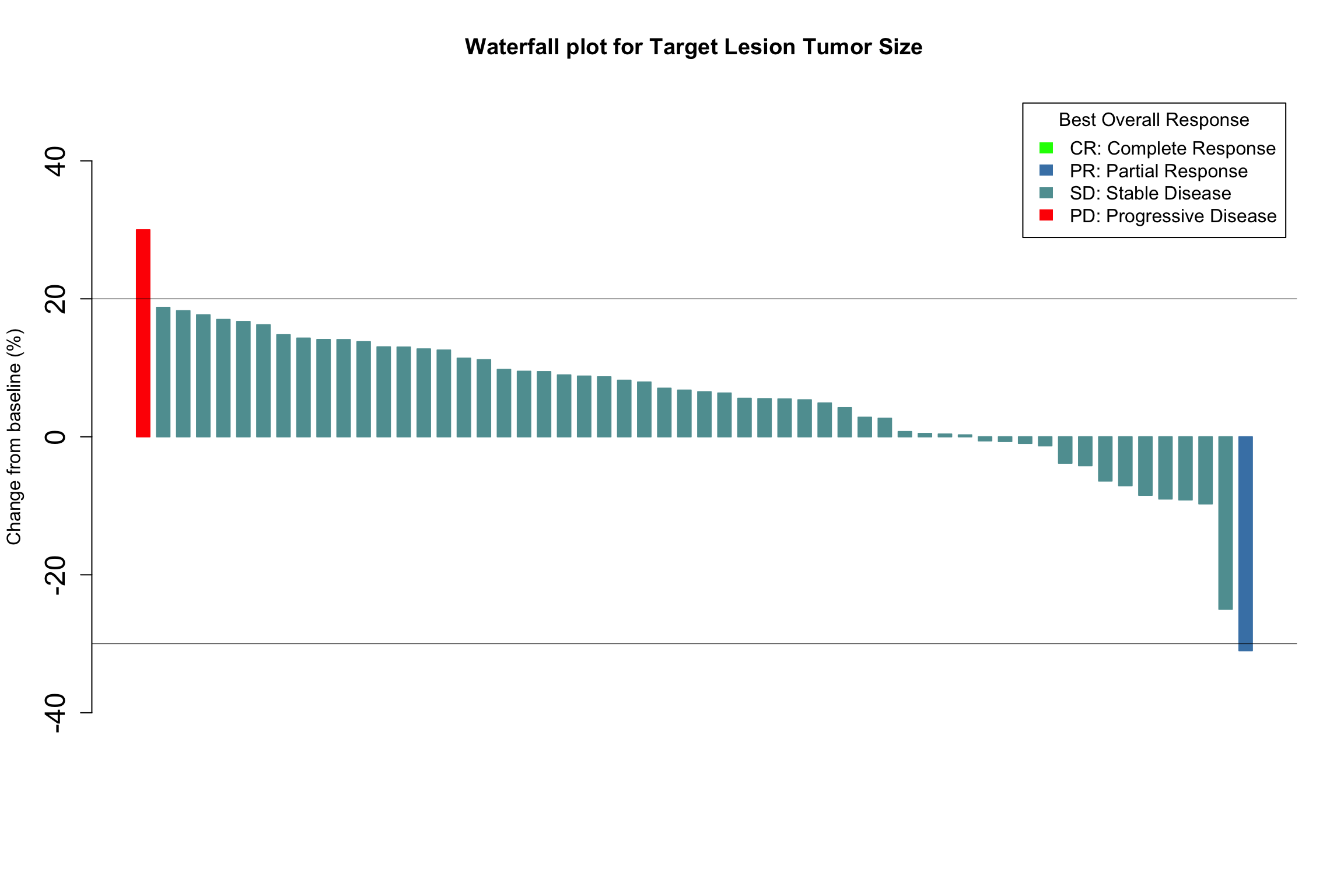

Take Home Points

High-quality data visualization of individual patient tumor responses to a study treatment can be displayed effectively for the cohort using waterfall plots.

As always, please reach out to us with thoughts and feedback

Session Info

sessionInfo()